Proof Qs (1 Viewer)

mmmmmmmmaaaaaaa · Jan 20, 2022

I am stuck on part (b) --> mainly for the proof for n=k+1 step

Screen Shot 2022-01-20 at 11.05.26 pm.png

ExtremelyBoredUser · Jan 26, 2022

mmmmmmmmaaaaaaa said:
I am stuck on part (b) --> mainly for the proof for n=k+1 step
View attachment 34731

(a)

Using a,b > 0

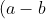$(a-b)(a^{n} - b^{n}) \geq 0$ , this works for a<b and b>a and you can convince yourself if you want. If b>a, both brackets will be negative and that will make a positive, if b<a then both brackets will be positive.

$a^{n+1} + b^{n+1} - b^{n}\times a - a^{n} \times b \geq 0$
$a^{n+1} + b^{n+1} \geq b^{n}\times a +a^{n} \times b$
as required.

(b)

$n = 1$ :

$\left( \frac{a+b}{2} \right)^{1} \ \leq \left( \frac{a^{1} +b^{1} }{2} \right)$

Hence n = 1 is true as equality holds for the inequality.

Assume k is a positive integer and true for n greater/equal to 1 (or whatever you write for assume stage, up to your discretion)

$n = k$ :

$\left( \frac{a+b}{2} \right)^{k} \ \leq \left( \frac{a^{k} +b^{k} }{2} \right)$ which will be our induction hypothesis

Now proving for $n = k + 1$ :

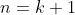
We need to prove this inequality; $\left( \frac{a+b}{2} \right)^{k+1} \ \leq \left( \frac{a^{k+1} +b^{k+1} }{2} \right)$

LHS:

$\left( \frac{a+b}{2} \right)^{k} \times \left( \frac{a+b}{2} \right)^{1} \ \leq \left( \frac{a^{k} +b^{k} }{2} \right) \times \left( \frac{a^{1} +b^{1} }{2} \right)$ from our induction hypothesis

= $\left( \frac{a^{k+1}+b^{k+1} + b^{k}\times a + a^{k} \times b}{4} \right)$ when expanding
= $\left( \frac{1}{2}\right) \times \left(\frac{a^{k+1}+b^{k+1} + b^{k}\times a + a^{k} \times b}{2} \right)$ (1)

We will use $a^{n+1} + b^{n+1} \geq b^{n}\times a +a^{n} \times b$ from (i) and substitute this into the eqn 1 to form a new inequality:

(1) <= $\left( \frac{1}{2}\right) \times \left(\frac{a^{k+1}+b^{k+1} +a^{k+1}+b^{k+1}}{2} \right)$
(1) <= $\left( \frac{1}{2}\right) \times \left(\frac{a^{k+1}+b^{k+1}}{1} \right)$

and we exactly got RHS of the original statement.

$\left( \frac{1}{2}\right) \times \left(\frac{a^{k+1}+b^{k+1}}{1} \right) \geq \left( \frac{1}{2}\right) \times \left(\frac{a^{k+1}+b^{k+1} + b^{k}\times a + a^{k} \times b}{2} \right) \geq \left( \frac{a+b}{2} \right)^{k+1} \$

Hence proven by the principles of mathematical induction (insert your own conclusion).

Make a Difference – Donate to Bored of Studies!

Proof Qs (1 Viewer)

mmmmmmmmaaaaaaa

Well-Known Member

ExtremelyBoredUser

Bored Uni Student

Users Who Are Viewing This Thread (Users: 0, Guests: 1)