Kurosaki
True Fail Kid
Hello BOS denizens  .
.
Do you know whether the HSC allows for combinatorial proofs when dealing with binomial coefficient identities?
e.g. Proving that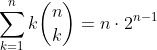
We can model this as creating a committee of size k people with a single chairperson, from a total amount of n people.
We can do this by: first choosing k people from n, then from those k people choosing a single person. Summing gives the LHS of the above expression.
Alternatively, choose one person to be the chairperson from the n people, done in n ways. Then for each subsequent person, they can either be in the committee or not, which accounts for the of the RHS. Multiplication principle gives the required expression.
of the RHS. Multiplication principle gives the required expression.
And as these 2 expressions are different ways of counting the same thing, they are equal.
Combinatorial proofs seem more natural to me than the mechanical method of considering a geometric series and comparing coefficients, and in some instances I find a bit faster as well..
Thanks in advance to anyone that helps with this!
Do you know whether the HSC allows for combinatorial proofs when dealing with binomial coefficient identities?
e.g. Proving that
We can model this as creating a committee of size k people with a single chairperson, from a total amount of n people.
We can do this by: first choosing k people from n, then from those k people choosing a single person. Summing gives the LHS of the above expression.
Alternatively, choose one person to be the chairperson from the n people, done in n ways. Then for each subsequent person, they can either be in the committee or not, which accounts for the
And as these 2 expressions are different ways of counting the same thing, they are equal.
Combinatorial proofs seem more natural to me than the mechanical method of considering a geometric series and comparing coefficients, and in some instances I find a bit faster as well..
Thanks in advance to anyone that helps with this!
Last edited:
