math help (1 Viewer)

Dashdorm24 · Jul 2, 2021

Screen Shot 2021-07-02 at 7.31.54 pm.png

Need any help on these 2 questions, for an upcoming assessment.

cossine · Jul 2, 2021

k = 1

you want to shift the curve 1 unit to the right. The graph P(x-k) is shifted k units to the right. So k = 1.

ii)
P(x) = (x+1)(x-2)^2

So just expand (x+1)(x-2)^2.

CM_Tutor · Jul 2, 2021

Actually, there are two possible values of $k$ ...

Dashdorm24 · Jul 3, 2021

CM_Tutor said:
Actually, there are two possible values of $k$ ...

and what would that be ?

cossine · Jul 3, 2021

Dashdorm24 said:
and what would that be ?

I think he is referring case of k = -2 which I missed.

To shift a graph k units to the left the transformation is f(x+k) where k is positive.

CM_Tutor · Jul 3, 2021

cossine said:
I think he is referring case of k = -2 which I missed.

To shift a graph k units to the left the transformation is f(x+k) where k is positive.

Yes, I am.

And @Dashdorm24, you can check each is valid by doing the transformation and seeing that the resulting $P(x)$ has $x$ as a factor.

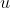
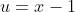
For example, taking $P(x) = (x + 1)(x - 2)^2$ (which is the same as $P(u) = (u + 1)(u - 2)^2$ , I'm just using $u$ as a dummy variable so that the transformation is clearer), and performing the transformation $u = x - 1$ , as suggested by @cossine, gives:

$\begin{align*} P(u) &= (u + 1)(u - 2)^2 \\ P(x - 1) &= \big[(x - 1) + 1\big]\big[(x - 1) - 2\big]^2 \quad \quad \text{putting $u = x - 1$} \\ &= x(x - 3)^2 \\ \text{So} \quad y &= x(x -3)^2 \quad \text{is the transformed polynomial} \end{align*}$

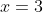
and it has a single root at the origin and a double root at $x = 3$ , just as would be expected from a shift of one unit to the right.

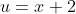
The second transformation, $u = x + 2$ , which @cossine correctly identified from my hint, should produce a shift of 2 units to the left, moving the double root to the origin. Checking:

$\begin{align*} P(u) &= (u + 1)(u - 2)^2 \\ P(x + 2) &= \big[(x + 2) + 1\big)\big[(x + 2) - 2\big]^2 \quad \quad \text{putting $u = x + 1$} \\ &= (x + 3)x^2 \\ \text{So} \quad y &= x^2(x +3) \quad \text{is the transformed polynomial} \end{align*}$

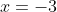
and it has a single root at $x = -3$ and a double root at the origin, just as would be expected from a shift of two units to the left.

Noting that our given polynomial $P(x) = (x + 1)(x - 2)^2$ has 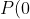$P(0) = 4$ , we can also predict that a shift downwards by 4 should give a transformed polynomial with a root at the origin. Check:

$\begin{align*} Q(x) &= (x + 1)(x - 2)^2 \\ P(x) + 4 &= (x + 1)(x - 2)^2 \quad \quad \text{putting $P(x) = Q(x) - 4$} \\ P(x) &= (x + 1)(x - 2)^2 - 4 \\ &= (x + 1)\left(x^2 - 4x + 4\right) - 4 \\ &= x^3 - 4x^2 + 4x + x^2 - 4x + 4 - 4 \\ &= x^3 - 3x^2 \\ \text{So} \quad P(x) &= x^2(x - 3) \quad \text{is the transformed polynomial} \end{align*}$

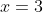
and it has a single root at $x = 3$ and a double root at the origin, just as would be expected from a shift of four units to the down. (The point $(3,\, 4)$ lies on the original polynomial, so a shift down of four should produce a root of the new polynomial at $x = 3$ .)

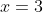
These techniques can be combined, along with dilations, to produce other polynomials as required.

math help (1 Viewer)

Dashdorm24

New Member

cossine

Well-Known Member

CM_Tutor

Moderator

Dashdorm24

New Member

cossine

Well-Known Member

CM_Tutor

Moderator

Users Who Are Viewing This Thread (Users: 0, Guests: 1)