This question is from the 2006 4U JRAHS Trial. I got part a) but for part b), my answer is 71'34'. I am confused about their solution and think it may not be correct. Could someone clarify please?
My solution gave that the truck starts at x=V^2sin(2theta)/3g, where y = the focus = -V^2cos(2theta)/2g. sub into eqn. I think it works when I graphed it here: https://www.desmos.com/calculator/kcbacwkxok
Question
(a) Ben’s Hot Wheel travels along an inclined ramp to jump over a truck. The Hot Wheel travels at an initial speed V m/s inclined at an angle θ to the horizontal at O, and acceleration due to gravity is g m/s2.
The Wheel’s trajectory is given by y = x tanθ − gx2 sec2 θ . 2V 2
θ
(i) Write this equation in the general form of a parabola: (x – h)2 = 4a(y − k), 3
where a, h, k are constants.
(ii) Calculate the angle of projection, θ, if the range is three times the width of 3
the truck and the top of the truck passes through the focus of equation in part (a).
Solution
Attached as a screenshot, due to formatting issues.
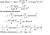

My solution gave that the truck starts at x=V^2sin(2theta)/3g, where y = the focus = -V^2cos(2theta)/2g. sub into eqn. I think it works when I graphed it here: https://www.desmos.com/calculator/kcbacwkxok
Question
(a) Ben’s Hot Wheel travels along an inclined ramp to jump over a truck. The Hot Wheel travels at an initial speed V m/s inclined at an angle θ to the horizontal at O, and acceleration due to gravity is g m/s2.
The Wheel’s trajectory is given by y = x tanθ − gx2 sec2 θ . 2V 2
θ
(i) Write this equation in the general form of a parabola: (x – h)2 = 4a(y − k), 3
where a, h, k are constants.
(ii) Calculate the angle of projection, θ, if the range is three times the width of 3
the truck and the top of the truck passes through the focus of equation in part (a).
Solution
Attached as a screenshot, due to formatting issues.

Last edited:
