Typing out the expressions will be too tedious for me.
Using the recurrence relation, iteratively:
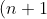I_n = 2ln2 - \frac {1}{n+1} - nI_{n-1} \\ \\ = (2ln2 - \frac {1}{n+1} - [2ln2 - \frac {1}{n} - (n-1)I_{n-2}]) \\ \\ = \frac {1}{n} - \frac {1}{n+1} + \left(2ln2 - \frac {1}{n-1} - [2ln2 - \frac{1}{n-2} - (n-3)I_{n-4}]\right)\\ \\ = \frac {1}{n-2} - \frac {1}{n-1} + \frac {1}{n} - \frac {1}{n+1} + (n-3)I_{n-4}\\ \\ = \frac {1}{n-2} - \frac {1}{n-1} +\frac {1}{n} - \frac {1}{n+1} + \left( 2ln2 - \frac {1}{n-3} - [2ln2 - \frac {1}{n-4} - (n-5)I_{n-6}] \right) )
In this way, if n is
odd:
The final
1I0 = 2ln2 - 1 will not be paired up within the big parentheses; its 2ln2 will cancel out the '2ln 2' from the 2I
1 term so that we have no '2ln 2' left.
So the case of n-odd is shown.
If n is
even:
The final
1I0 will be within the final big parentheses, so that its '2 ln 2' remains (
uncancelled) so that we end up with the formula for n-even.