1. The parabola
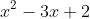
is negative when
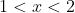
. So when you take the absolute value, the only change in the graph is that that area will be flipped across the x axis to become positive. Same area, just the direction is changed. Therefore, to obtain the area between
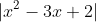
and the x-axis from
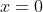
to
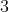
, we can integrate three parts of the curve separately (not to be confused with integration by parts...):

Normally the middle integral would be negative, since the curve is under the x-axis at that point, but we can just take the absolute value.
________________________________________________________________________________
2. It may be less confusing to integrate on the x-axis, but it doesn't matter which you pick, you just have to rearrange both equations in terms of the same variable.
The parabola
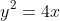
is just the parabola
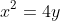
rotated 90 degrees clockwise about the origin.
To obtain the area where they intersect, we can rearrange
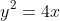
to make
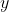
the subject, giving
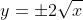
. Since these parabolas never intersect below the x-axis, we actually don't need the
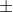
sign so we can remove it and take the positive root.
Clearly, these integrals intersect at the origin and one other point, which is
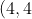)
. Therefore (keeping in mind which curve is above the other) we can use the integral
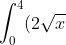 - \left(\frac{1}{4}x^2\right) \, dx)
________________________________________________________________________________
3. If you draw a quick sketch it's easy to see that you are essentially being asked to find the area between
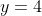
and
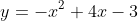
from
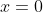
to
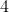
.
The integral we need is just
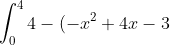 \, dx)
