for LHS > MHS,
(a+b)(1/a+1/b) > 4
1/a + 1/b > 4/(a+b)
1/2(1/a + 1/b) > 2/(a+b)
similarly,
1/2(1/b+1/c) > 2/(b+c)
1/2(1/c+1/a) > 2/(c+a)
adding these, simplifying and factorising gives:
1/a + 1/b + 1/c > 2[1/(a+b) + 1/(b+c) + 1/(c+a)]
hence LHS > MHS
for MHS > RHS,
[(a+b)+(b+c)+(c+a)][1/(a+b)+1/(b+c)+1/(c+a)] > 9
2(a+b+c)[1/(a+b)+1/(b+c)+1/(c+a)] > 9
2[1/(a+b)+1/(b+c)+1/(c+a)] > 9/(a+b+c)
hence
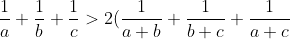 > \dfrac{9}{a+b+c} )
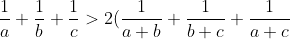 > \dfrac{9}{a+b+c} )