mr.habibbi
Member
- Joined
- Oct 27, 2019
- Messages
- 41
- Gender
- Male
- HSC
- 2021
Students helping students, join us in improving Bored of Studies by donating and supporting future students!
what book is this?Hi all,
This has been a tricky question that ive been stuck on for a while, not sure if its even possible.
View attachment 31305
If you manage to get it please share the solutions.
Is the answer t = 40/k? I am unsure of my working out but I pretty much substituted the results of the integrand for both x and t. Could you give an update.Hi all,
This has been a tricky question that ive been stuck on for a while, not sure if its even possible.
View attachment 31305
If you manage to get it please share the solutions.
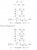

do u ahve another solution after the editView attachment 31490
View attachment 31492
I'm not sure if these calculations are eligible or correct and I might be doing something wrong so please feel free to check.
To clarify;
The net force equation was found through the diagram considering the weight force on the mass hanging from the pulley and the 2 resistive forces on both masses.
The equation for acceleration was found through substituting F in the force equation with ma and dividing both sides by 20 since the collective mass was 20kg.
EDIT:
I realized I made a mistake when calculating the first equation, I didn't consider the -v on top.
upon reading it again, u did what i thought would be the reason that it wouldnt work haha.View attachment 31490
View attachment 31492
I'm not sure if these calculations are eligible or correct and I might be doing something wrong so please feel free to check.
To clarify;
The net force equation was found through the diagram considering the weight force on the mass hanging from the pulley and the 2 resistive forces on both masses.
The equation for acceleration was found through substituting F in the force equation with ma and dividing both sides by 20 since the collective mass was 20kg.
EDIT:
I realized I made a mistake when calculating the first equation, I didn't consider the -v on top.
Yeah that was the only thing I thought of because I didn't know what to do with k because it doesn't really show a way or specify like most normal questions. I realised that as well after posting it with the fact I didn't integrate the first one. I can provide another solution through substituting k in each equation and have the constants with different letters to distinguish them but I doubt the equation would be the correct answer but the working out would be logical.upon reading it again, u did what i thought would be the reason that it wouldnt work haha.
The two C's are different, and do not necessarily cancel each other out.
Yeah I got that same equation first I think but I didnt know what to do with velocity part so I just tried the method I posted above, idek what to do next because the calculation I did was the closest I got? . I reintegrated the first equation and I got x = −490ln(|kx−49|)+10kx/k^2+C but I cant be bothered at this point to go further with substitution since there's no limits given, and idkdk pointed out the C's were different so if you found an equation for k and substituted into the x or t equation you could work out the final equation with multiple variables (Two different C's) and so on but not sure that would suffice as an answer with that much unknown variables.pre sure this q is impossible unless there's a trick
Ive gotten to the equation 40k=T-v where v is final speed.
how did u get rid of Cpre sure this q is impossible unless there's a trick
Ive gotten to the equation 40k=T-v where v is final speed.
You sub in the bounds of integration. never use the constant method I always put the bounds in. This case it's v=0 --> v and x = 0 --> 40.how did u get rid of C
i think so but does that help?Given they are attached by a string of fixed length and that it will always be taut, won't the two masses always have the same speed?
Energy cant be mechanical if theres resistance.Hey guys, this solution might be really whacky and possibly wrong. I wasn't satisfied with the unknown variables so I decided to solve this problem without calculus. The first idea that popped up to my head is instead of using forces, using ME to solve the problem.
The work done by the object is:
W = Fs, where F is force, s is displacement.
Law of Conservation states; ME = U + KE (Mechanical Energy = Gravitational Potential Energy + Kinetic Energy)
At x = 40, the Kinetic Energy of the object is 0 as there is no motion at this point. At this point in time, the position of the blocks resemble the diagram. Blue is the farthest away from the pulley and the red is at its highest point.
U = mgh = 10*9.8*40 = 98*40 = 3920
U = ME at this point. 3920J
So now calculating the Kinetic Energy when U = 0, aka when x = 0 (height is 0) (THIS IS NOT TO SAY THAT THE RED OBJECT HIT THE GROUND, THIS IS SIMPLY WHEN THE BLUE OBJECT REACHED 40m) KE = 1/2 * m * v^2
U + KE = ME
KE + 0 = 3920
5*v^2 = 3920 therefore v = 28 instantaneously at x = 0
The velocity of both objects are identical - and this can be inferred mathematically through the identical acceleration and resistive force, the objects in the system share identical properties and as so at this point we can extrapolate the speed of the blue object.
So using this knowledge. We can simply calculate the time at when the velocity is 28 since it is the instantaneous final velocity (before blue falls off):
v = s/t
t= s/v
t = 40/28
t = 1.43s
At this point the blocks can no longer move since the blue block reached its maximum distance and if the pulley is disregarded as an object blocking the Blue box from falling, it would have fell off the plane at approx t = 1.43s) This solution is made possible mainly from the fact that these objects have identical properties - if they did not, then I doubt it would be solvable?
rip there goes that try. Im not sure what else to do. I re-read the question and I guess you could take the bounds from 0 to 40 and try something there but I'm not sure what other method you could use.Energy cant be mechanical if theres resistance.
So is my previous answer incorrect?rip there goes that try. Im not sure what else to do. I re-read the question and I guess you could take the bounds from 0 to 40 and try something there but I'm not sure what other method you could use.
I think its the most correct as of now because I don't see anything wrong with the calculation . I was just trying to find an answer without unknown variables. Perhaps there is prior context for the question where you get more info.So is my previous answer incorrect?
