What do you do when you encounter a question during an exam, and the question is flawed and you realise it is flawed?
For example, I have just come across the following question:
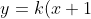(x - 1))
where and
and 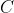 is an arbitrary constant of integration. Though not directly stated, it follows from this definition that
is an arbitrary constant of integration. Though not directly stated, it follows from this definition that 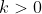 .
.
However:
 \qquad \qquad \text{where $k \in \mathbb{R} \neq 0$} \\ &= kx^2 - k \\ \text{Thus, LHS } = \cfrac{dy}{dx} &= 2kx - 0 \\ &= 2x \times \cfrac{y}{x^2 - 1} \qquad \qquad \text{on making $k\neq 0$ the subject of $y = k(x^2 - 1)$} \\ &= \cfrac{2xy}{x^2 - 1} \qquad \qquad \text{noting that the substitution requires $x^2 \neq 1$} \\ &=\ \text{RHS} \end{align*})
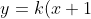(x - 1)) where
where  and is restricted to the domain
and is restricted to the domain 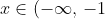\cup(-1,\,1)\cup(1,\,\infty))
which includes the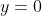 horizontal line solution as
horizontal line solution as  .
.
Providing the correct solution would be time consuming, but worse, the question continues to two more parts:
 where
where 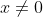
which is a relation, even though is expressed as a function of
is expressed as a function of  . Presumably they mean the answer to be
. Presumably they mean the answer to be
 where
where 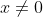
so that the curve does pass through (1, 1).
}{1 - x^2} = -1)
and concludes
 and
and  .
.
Further, the function from part (ii) is a particular solution of the DE, and is only defined for) (it is even, I graphed it in DESMOS).
(it is even, I graphed it in DESMOS).
Having tried various approaches in DESMOS, I think what is being established is about the points of intersection::
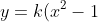 = \sqrt{\ln{|x|} - \cfrac{x^2 - 3}{2}}) has two solutions,
has two solutions, 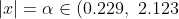)
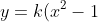 = \pm\sqrt{\ln{|x|} - \cfrac{x^2 - 3}{2}}) has four solutions,
has four solutions, $})
I'm interested in thoughts about this example, but more generally about the situation of a flawed exam question. So, restating my original question:
What do you do when you encounter a question during an exam, and the question is flawed and you realise it is flawed?
For example, I have just come across the following question:
The solutions take the usual approach to a separable DE to get(i) Show that the differential equation
describes a family of parabolas with x-intercepts at (1, 0) and (-1, 0).
where
However:
- equations of the form
with
also satisfy the DE (and the question)
- the line
is also a valid solution of the DE as it yields
, which is the gradient function of
(depending on the domain - see next point), but this is inconsistent with the question
- the given points (1, 0) and (-1, 0) can't be x-intercepts of any parabola with a vertical axis of symmetry and satisfy this DE because the parabola would have a slope that is finite and real (namely
in the solution's case), yet the coordinates themselves make
undefined... so the question's "family of parabolas" must exclude these points and thus have no x-intercepts!
- in fact, (1, 0) and (-1, 0) can only lie on any solution of the DE if the curve is vertical at these points (and thus, they are vertical inflexions)... this excludes them even from the trivial
solution
which includes the
Providing the correct solution would be time consuming, but worse, the question continues to two more parts:
The answer given isNow consider the differential equation
Find the equation of the curve which satisfies this differential equation and passes through the point (1, 1). Express your answer as a function of.
which is a relation, even though
so that the curve does pass through (1, 1).
The solution states that multiplying the DEs yields(iii) What can be said about the gradient of the curve in part (ii) in relation to the family of curves in part (i)?
and concludes
Now, the multiplication given is only defined ifSince the two are gradient functions and when multiplied the product is −1, the gradient of curve in part ii), that is the tangent, is always perpendicular to the family of curves in part i).
Further, the function from part (ii) is a particular solution of the DE, and is only defined for
Having tried various approaches in DESMOS, I think what is being established is about the points of intersection::
- for every
, the equation
- for every
, the equation
- at these two points of intersection
, or four points of intersection
and
(if the relation solution to the DE is chosen), the curves are perpendicular... that is, at every intersection, the tangent to the parabola is the normal to the particular solution from (ii)
I'm interested in thoughts about this example, but more generally about the situation of a flawed exam question. So, restating my original question:
What do you do when you encounter a question during an exam, and the question is flawed and you realise it is flawed?
