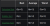
The main ways of comparing sorts would be run-time (worst case, best case + average, constant factors + real world performance), memory usage, stability, parallelisation and if they are online or offline. For SDD, I would probably focus on best case run time, the behaviour for pre-sorted arrays and the constant factors.
The sort algorithms in the SDD syllabus are quite basic, so worst case run time performance (often the focus in an undergraduate class) is not too useful as they can all regress to needing to compare each pair (
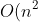)
). The best case run time for arrays that are already sorted (or mostly sorted) is interesting for comparison however as this is a common input.
Constant factors and real world performance are where certain algorithms appear to be academically better or equivalent when using Big-O analysis, but require a lot of work at each step (high constant factors) or cause frequent CPU cache hit misses. CPU cache hits I believe would be beyond the scope of SDD.
For simple sorting algorithms, memory usage will only differ if an algorithm works in place (uses the input array) or requires creating a new array. Parallelisation would be out of scope of the SDD syllabus, and none of these algorithms use divide and conquer.
Stability is an important concept for sorting. In SDD, you are generally sorting numbers, but in practice we usually sort objects by one or more fields on the object. When sorting objects, if there is a tie between two objects, often we want to retain the original order. This may be out of scope for SDD.
Online vs offline compares if an algorithm is able to operate on data as it is received, or if we require the entire input upfront. This is useful if the data is being streamed from a database or some kind of live data feed.
Selection Sort is probably the most naive algorithm. It builds up a sorted portion of the array by trying to pick the smallest element from the unsorted part of the array and extending the sorted part of the array by swapping this selected element with the unsorted element currently in that position.
As it has to find the minimum at each iteration, even for a pre-sorted array, it will have an
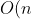*O(n) = O(n^2))
best case.
Since it swaps elements across the array (e.g. first element may move to the end), it is not a stable sort as it won't retain the original order for ties. As it requires finding the global minimum (or maximum) of the array, it is also an offline algorithm as it is not robust to a new minimum arriving.
Insertion sort processes elements one by one and builds up a sorted part of the array. The element being processed is put in place in the sorted portion of the array, some sorted elements will be shifted up a position to fill the gap created by removing the first unsorted element.
If the array is already in order, the process of "building" the sorted array will just involve an
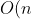)
scan over the whole array with no swaps. It is an online algorithm as receiving new elements as we are sorting does not affect the operation of the algorithm.
A particularly naive implementation of either Selection or Insertion sort might make a new array entirely for the sorted portion (i.e. not in place), but they can both be implemented in-place and therefore are fairly memory efficient.
Bubble sort scans through the input scanning adjacent pairs and swapping any that are out of order. Each iteration will result in 1 extra element at the end being in the correct order. Repeat until no swapping occurs (upper bound by the input count), which means it can terminate with a single iteration for a pre-sorted array.
Bubble sort on paper has the same runtime characteristics as a insertion sort, but in practice the bubble sort has higher constant factors as it performs more comparisons. This video demonstrates it well:
Since bubble sort uses the input array, it's an in-place sort and memory efficient. Since it compares and swaps only adjacent pairs, it is a stable sort. Since bubble sort generally has an optimisation that assumes part of the array is sorted and fixed in place, this make it an offline algorithm.