9 Complex/Ellipse Questions help please ASAP!!! (1 Viewer)
- Thread starter Accuracy
- Start date
deswa1
Well-Known Member
- Joined
- Jul 12, 2011
- Messages
- 2,256
- Gender
- Male
- HSC
- 2012
1) i)Cuts the x axis when y=0. Therefore at -2,0,2.
iii) Using product rule+chain rule
<a href="http://www.codecogs.com/eqnedit.php?latex=y=x\sqrt{4-x^2} \\\frac{dy}{dx}=\sqrt{4-x^2}-\frac{x^2}{\sqrt{4-x^2}}\\ \frac{dy}{dx}=\frac{4-2x^2}{\sqrt{4-x^2}}\\ \frac{dy}{dx}=\frac{2(2-x^2)}{\sqrt{4-x^2}}" target="_blank"><img src="http://latex.codecogs.com/gif.latex?y=x\sqrt{4-x^2} \\\frac{dy}{dx}=\sqrt{4-x^2}-\frac{x^2}{\sqrt{4-x^2}}\\ \frac{dy}{dx}=\frac{4-2x^2}{\sqrt{4-x^2}}\\ \frac{dy}{dx}=\frac{2(2-x^2)}{\sqrt{4-x^2}}" title="y=x\sqrt{4-x^2} \\\frac{dy}{dx}=\sqrt{4-x^2}-\frac{x^2}{\sqrt{4-x^2}}\\ \frac{dy}{dx}=\frac{4-2x^2}{\sqrt{4-x^2}}\\ \frac{dy}{dx}=\frac{2(2-x^2)}{\sqrt{4-x^2}}" /></a>
iii) Using product rule+chain rule
<a href="http://www.codecogs.com/eqnedit.php?latex=y=x\sqrt{4-x^2} \\\frac{dy}{dx}=\sqrt{4-x^2}-\frac{x^2}{\sqrt{4-x^2}}\\ \frac{dy}{dx}=\frac{4-2x^2}{\sqrt{4-x^2}}\\ \frac{dy}{dx}=\frac{2(2-x^2)}{\sqrt{4-x^2}}" target="_blank"><img src="http://latex.codecogs.com/gif.latex?y=x\sqrt{4-x^2} \\\frac{dy}{dx}=\sqrt{4-x^2}-\frac{x^2}{\sqrt{4-x^2}}\\ \frac{dy}{dx}=\frac{4-2x^2}{\sqrt{4-x^2}}\\ \frac{dy}{dx}=\frac{2(2-x^2)}{\sqrt{4-x^2}}" title="y=x\sqrt{4-x^2} \\\frac{dy}{dx}=\sqrt{4-x^2}-\frac{x^2}{\sqrt{4-x^2}}\\ \frac{dy}{dx}=\frac{4-2x^2}{\sqrt{4-x^2}}\\ \frac{dy}{dx}=\frac{2(2-x^2)}{\sqrt{4-x^2}}" /></a>
hey, the answers for 1) only have -2 and 2. theres no zero for some reason :S1) i)Cuts the x axis when y=0. Therefore at -2,0,2.
iii) Using product rule+chain rule
<a href="http://www.codecogs.com/eqnedit.php?latex=y=x\sqrt{4-x^2} \\\frac{dy}{dx}=\sqrt{4-x^2}-\frac{x^2}{\sqrt{4-x^2}}\\ \frac{dy}{dx}=\frac{4-2x^2}{\sqrt{4-x^2}}\\ \frac{dy}{dx}=\frac{2(2-x^2)}{\sqrt{4-x^2}}" target="_blank"><img src="http://latex.codecogs.com/gif.latex?y=x\sqrt{4-x^2} \\\frac{dy}{dx}=\sqrt{4-x^2}-\frac{x^2}{\sqrt{4-x^2}}\\ \frac{dy}{dx}=\frac{4-2x^2}{\sqrt{4-x^2}}\\ \frac{dy}{dx}=\frac{2(2-x^2)}{\sqrt{4-x^2}}" title="y=x\sqrt{4-x^2} \\\frac{dy}{dx}=\sqrt{4-x^2}-\frac{x^2}{\sqrt{4-x^2}}\\ \frac{dy}{dx}=\frac{4-2x^2}{\sqrt{4-x^2}}\\ \frac{dy}{dx}=\frac{2(2-x^2)}{\sqrt{4-x^2}}" /></a>
nightweaver066
Well-Known Member
- Joined
- Jul 7, 2010
- Messages
- 1,585
- Gender
- Male
- HSC
- 2012
2) ii) ^n)

 = 0)
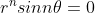
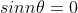
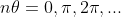

nightweaver066
Well-Known Member
- Joined
- Jul 7, 2010
- Messages
- 1,585
- Gender
- Male
- HSC
- 2012
x = 0 is an x-intercept.hey, the answers for 1) only have -2 and 2. theres no zero for some reason :S

Carrotsticks
Retired
- Joined
- Jun 29, 2009
- Messages
- 9,494
- Gender
- Undisclosed
- HSC
- N/A
Question 1
(i) Let y=0 and solve. x=0 (double root) and x= plus/minus 2
(iii) Differentiate it using the product rule.
Question 2
(ii) z = sqrt(2) cis (pi/12). We want it to be real (this will first occur when the argument is pi), so we multiply by itself 12 times to get it to be a real number ie: n=12.
Question 3
(iv) Arg(z) is -pi/3. We want to rotate the vector N times such that it becomes itself (perhaps with different magnitude, but we are only looking at the argument). Obviously this will occur if we go backwards by pi/3 exactly 7 times (equivalent of a 360 degree rotation). So N=7.
Question 4
(ii) The first locus is a circle centred at (0,2) with radius k. The second locus is a circle centred at (3,2) and radius 2. So the 'endpoints' of the circle occur at (1,2) and (5,2). The two circles will intersect at two points if the radius of the first locus is big enough (but not too big). Clearly this will only work if the first locus has radius *slightly* bigger than 1 or *slightly* less than 5. If you draw a sketch, you will see this clearly. I say 'slightly' because when it is equal to 1 and 5, it will intersect at only ONE point (tangential). So our answer is 1 < k < 5.
Question 5
(i)
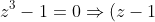(z^2 + z + 1) = 0 $ upon factorising. But remember that w is the COMPLEX root, so we can't have the $ (z-1) $ part since that yields a real solution, so therefore the other part must be equal to 0 ie: $ w^2 + w + 1 =0)
(ii)
^2(1-w^2)^2 $ and use part (i) to finish the question.$ )
Question 6
 = k \times arg(z(z-2)) = k \times \left [ arg(z) + arg(z-2) \right ] = k \times arg(z) + k \times arg(z-2) = arg(z-2) \Rightarrow k = \frac{arg(z-2)}{arg(z-2)+arg(z)})
Question 7
P is the same as z_1 plus z_1 rotated 90 degrees. But z_1 rotated 90 degrees is the same as z_1 times i. Therefore P = z_1 + iz_1 = (1+i)z_1
Question 8
(i) z_1 + z_2 is a vector exactly between z_1 and z_2. From the diagram, it looks like the argument will be a little bit less than 90 degrees. z_1 - z_2 is the vector pointing from z_2 to z_1.
(ii) From the question, we know that:
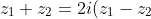 $ which means that the vectors $ z_1 + z_2 $ and $ z_1 - z_2 $ are exactly 90 degrees apart (due to multiplication by i) such that $ z_1+z_2 $ is twice as long as $ z_1 - z_2 . $ But the only quadrilateral with the diagonals (remember that $ z_1 + z_2 $ and $ z_1 - z_2 $ are the diagonals) perpendicular to each other is a rhombus ie: all sides are equal ie: $ |z_1| = |z_2| )
(iii) As I said before, the vector z_1 + z_2 is twice as long as z_1 - z_2. Draw the rhombus and label the intersection to be perpendicular (property of a rhombus). Label alpha. alpha/2 is just half the angle in between. Use SOH CAH TOA with alpha/2 to get the identity:

(i) Let y=0 and solve. x=0 (double root) and x= plus/minus 2
(iii) Differentiate it using the product rule.
Question 2
(ii) z = sqrt(2) cis (pi/12). We want it to be real (this will first occur when the argument is pi), so we multiply by itself 12 times to get it to be a real number ie: n=12.
Question 3
(iv) Arg(z) is -pi/3. We want to rotate the vector N times such that it becomes itself (perhaps with different magnitude, but we are only looking at the argument). Obviously this will occur if we go backwards by pi/3 exactly 7 times (equivalent of a 360 degree rotation). So N=7.
Question 4
(ii) The first locus is a circle centred at (0,2) with radius k. The second locus is a circle centred at (3,2) and radius 2. So the 'endpoints' of the circle occur at (1,2) and (5,2). The two circles will intersect at two points if the radius of the first locus is big enough (but not too big). Clearly this will only work if the first locus has radius *slightly* bigger than 1 or *slightly* less than 5. If you draw a sketch, you will see this clearly. I say 'slightly' because when it is equal to 1 and 5, it will intersect at only ONE point (tangential). So our answer is 1 < k < 5.
Question 5
(i)
(ii)
Question 6
Question 7
P is the same as z_1 plus z_1 rotated 90 degrees. But z_1 rotated 90 degrees is the same as z_1 times i. Therefore P = z_1 + iz_1 = (1+i)z_1
Question 8
(i) z_1 + z_2 is a vector exactly between z_1 and z_2. From the diagram, it looks like the argument will be a little bit less than 90 degrees. z_1 - z_2 is the vector pointing from z_2 to z_1.
(ii) From the question, we know that:
(iii) As I said before, the vector z_1 + z_2 is twice as long as z_1 - z_2. Draw the rhombus and label the intersection to be perpendicular (property of a rhombus). Label alpha. alpha/2 is just half the angle in between. Use SOH CAH TOA with alpha/2 to get the identity:

Last edited:
nightweaver066
Well-Known Member
- Joined
- Jul 7, 2010
- Messages
- 1,585
- Gender
- Male
- HSC
- 2012
Carrot, for question 3, isn't it n = 7?
Carrotsticks
Retired
- Joined
- Jun 29, 2009
- Messages
- 9,494
- Gender
- Undisclosed
- HSC
- N/A
Yep that's right. I forgot that n=1 yields the identity vector.Carrot, for question 3, isn't it n = 7?
I just remembered, I made this exact same mistake a couple months ago!
Somebody do Q9 for me please, I'm too tired now.
And to answer your wall-post question Accuracy, z-1 yields a real solution because when z - 1 = 0, then z = 1 (which is real).
Last edited:
nightweaver066
Well-Known Member
- Joined
- Jul 7, 2010
- Messages
- 1,585
- Gender
- Male
- HSC
- 2012
9) 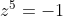
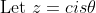
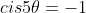
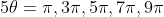
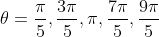
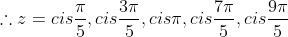

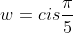


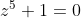

(w^4 - w^3 + w^2 - w + 1) = 0)
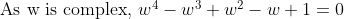
Last edited:
nightweaver066
Well-Known Member
- Joined
- Jul 7, 2010
- Messages
- 1,585
- Gender
- Male
- HSC
- 2012
Haha i don't know why i said 5..^That's question 9, not 5
bleakarcher
Active Member
- Joined
- Jul 8, 2011
- Messages
- 1,509
- Gender
- Male
- HSC
- 2013
Carrot, your not completely done with q6. You have to use geometry to find a relationship between the two arguments.Question 1
(i) Let y=0 and solve. x=0 (double root) and x= plus/minus 2
(iii) Differentiate it using the product rule.
Question 2
(ii) z = sqrt(2) cis (pi/12). We want it to be real (this will first occur when the argument is pi), so we multiply by itself 12 times to get it to be a real number ie: n=12.
Question 3
(iv) Arg(z) is -pi/3. We want to rotate the vector N times such that it becomes itself (perhaps with different magnitude, but we are only looking at the argument). Obviously this will occur if we go backwards by pi/3 exactly 7 times (equivalent of a 360 degree rotation). So N=7.
Question 4
(ii) The first locus is a circle centred at (0,2) with radius k. The second locus is a circle centred at (3,2) and radius 2. So the 'endpoints' of the circle occur at (1,2) and (5,2). The two circles will intersect at two points if the radius of the first locus is big enough (but not too big). Clearly this will only work if the first locus has radius *slightly* bigger than 1 or *slightly* less than 5. If you draw a sketch, you will see this clearly. I say 'slightly' because when it is equal to 1 and 5, it will intersect at only ONE point (tangential). So our answer is 1 < k < 5.
Question 5
(i)
(ii)
Question 6
Question 7
P is the same as z_1 plus z_1 rotated 90 degrees. But z_1 rotated 90 degrees is the same as z_1 times i. Therefore P = z_1 + iz_1 = (1+i)z_1
Question 8
(i) z_1 + z_2 is a vector exactly between z_1 and z_2. From the diagram, it looks like the argument will be a little bit less than 90 degrees. z_1 - z_2 is the vector pointing from z_2 to z_1.
(ii) From the question, we know that:
(iii) As I said before, the vector z_1 + z_2 is twice as long as z_1 - z_2. Draw the rhombus and label the intersection to be perpendicular (property of a rhombus). Label alpha. alpha/2 is just half the angle in between. Use SOH CAH TOA with alpha/2 to get the identity:

Carrotsticks
Retired
- Joined
- Jun 29, 2009
- Messages
- 9,494
- Gender
- Undisclosed
- HSC
- N/A
k = 2/3 haha.Carrot, your not completely done with q6. You have to use geometry to find a relationship between the two arguments.
Also next time, best not quote a huge bit of text like that. Looks a bit messy.
bleakarcher
Active Member
- Joined
- Jul 8, 2011
- Messages
- 1,509
- Gender
- Male
- HSC
- 2013
meh. ^
Carrotsticks
Retired
- Joined
- Jun 29, 2009
- Messages
- 9,494
- Gender
- Undisclosed
- HSC
- N/A
umm what
Banned
when u replace it with argument of complex number, how do u find "n"?
2) ii)

nightweaver066
Well-Known Member
- Joined
- Jul 7, 2010
- Messages
- 1,585
- Gender
- Male
- HSC
- 2012
when u replace it with argument of complex number, how do u find "n"?










