The horizontal range of the ball is maximised when
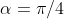
. This can be easily shown by examining the equation in ii).
Case 1: The ceiling allows for an angle of projection of 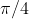 .
.
If the ceiling allows for at least this angle of projection, then
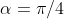
is the optimal angle to throw the ball.
It doesn't matter how tall the ceiling is after a certain point - because the best angle is
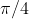
and any higher angle will simply lower
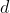
.
The horizontal range obtained by projecting at this optimal angle is then

.
But when does the ceiling allow for this angle? It is when the maximum height of the projectile (with angle of projection
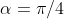
) is less than or equal to the height allowed by the ceiling (which is
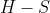
).
Mathematically, this can be represented by the condition
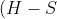 \geq \frac{v^2 \sin^2 (\pi/4)}{2g} \implies 4g(H-S) \geq v^2)
.
Case 2: The ceiling does NOT allow for an angle of projection of 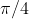 .
.
As
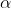
decreases past
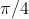
, so too does
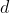
, from ii).
Therefore we want the largest value of
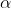
we can get. This value occurs when the tip of the ball's trajectory coincides with the ceiling, i.e.
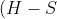 = \frac{v^2 \sin^2 \alpha}{2g})
Rearrangement gives:
}{v^2} \implies \sin \alpha = \sqrt{\frac{2g(H-S)}{v^2}} \quad (1))
}{v^2} \implies \cos \alpha = \sqrt{\frac{v^2 - 2g(H-S)}{v^2}} \quad (2))
Finally, to get the answer, substitute (1) and (2) into:
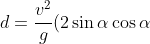)


