Solving trigonometric functions Multiple choice HSC (2 Viewers)

[BlueGas]

I need help with with this question, I don't know how to do this and I need someone to simply explain how to do this, thanks!

I did inverse tan(-1/Root3) and that gave me -30 but none of the answers were related to -30.

 

[InteGrand]

I did inverse tan(-1/Root3) and that gave me -30 but none of the answers were related to -30.

The reason that none of the answers is -30º is that the inverse tan function always returns angles between -90º and +90º, since the tan function is restricted to the domain -90º < x < 90º to make it have an inverse, because if we didn't restrict the domain, the function wouldn't be invertible, as it isn't one-to-one otherwise. (This is taught in the 3U course.)

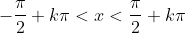
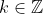
So the -30º you got is the unique angle x in the domain -90º ≤ x ≤ 90º that makes tan x equal -1/√3. Note that in each "branch" of the tan function (see the graph of it: http://www.analyzemath.com/trigonometry/graph_tangent.gif; each branch is a domain of the form , for (integers)), there will be exactly one angle (x-value) that makes the tan function take on a given value (in our case -1/√3). We want angles that fall between 0 and 360º. 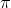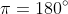Since the tan function has a period of (that is, it repeats its value every time you increase/decrease the x-value by ), if we know one solution, we know that any multiple of 180º added to this solution is also a solution. Since we know one solution is -30º, we know the following are also solutions:

-30º±180º, -30º±2•(180º), -30±3•(180º), and so on.

Only two of these will fall between 0 and 180º, so we only select those ones since we are only asked to find the solutions in this particular interval.

 

[InteGrand]

So in general, if asked for solutions of something like , where is some given real number, there will not just be one solution, but infinitely many solutions, and they will be of the form , where k is an integer.

(This is taught in the HSC 3U course.)

 

[Feynman]

Find the general angle which is 30 degrees. Then use the ASTC rule to see where the tan function is negative (i.e. 2nd and 4th). From there find the obtuse angles by subtracting 30 degrees from the x axis, 180 - 30 and 360 - 30, to get the values 150 degrees and 330 degrees. Convert these to rad and you have the answer.

 

[BlueGas]

Find the general angle which is 30 degrees. Then use the ASTC rule to see where the tan function is negative (i.e. 2nd and 4th). From there find the obtuse angles by subtracting 30 degrees from the x axis, 180 - 30 and 360 - 30, to get the values 150 degrees and 330 degrees. Convert these to rad and you have the answer.

Thanks man, I understand the process now, but one last question just to make sure, If I got sin 30, sin is positive in A and S, do I do 0 + 30 or 90-30? And in the S quadrant, do I do 90 + 30 or 180 - 30?

 

[Crisium]

This is a bit worrying seeing as you're more than half way through year 12 :/

You should revise year 11 trigonometry because learning how to do these types of questions is very important

 

[Crisium]

Thanks man, I understand the process now, but one last question just to make sure, If I got sin 30, sin is positive in A and S, do I do 0 + 30 or 90-30? And in the S quadrant, do I do 90 + 30 or 180 - 30?

Assuming you mean inverse sin(0.5) , the immediate value will be positive and it will most likely be in the given domain - So leave it as it is (This is your first solution)

You then use ASTC to see in which quadrant sin is positive (i.e. The Second Quadrant)

You then do 180 - (Positive Value Above)

You will then get your second answer and if it is in the given domain then keep this

Those should be your two solutions

 

[InteGrand]

Assuming you mean inverse sin30 , the immediate value will be positive and it will most likely be in the given domain - So leave it as it is (This is your first solution)

You then use ASTC to see in which quadrant sin is positive (i.e. The Second Quadrant)

You then do 180 - (Positive Value Above)

You will then get your second answer and if it is in the given domain then keep this

Those should be your two solutions

We can't take the inverse sine of 30, since the output (range) of the sine function is between -1 and +1 (which 30 is not).

I think what was meant was what should be done if he got an answer of 30º by taking the inverse sine of something (which would have been ).

 

[Crisium]

We can't take the inverse sine of 30, since the output (range) of the sine function is between -1 and +1 (which 30 is not).

I think what was meant was what should be done if he got an answer of 30º by taking the inverse sine of something (which would have been ).

Oh crap

Yeah I meant 0.5

 

[Feynman]

Thanks man, I understand the process now, but one last question just to make sure, If I got sin 30, sin is positive in A and S, do I do 0 + 30 or 90-30? And in the S quadrant, do I do 90 + 30 or 180 - 30?

Angle should always touch the x-axis:

First quadrant is normal
Second quadrant is 180 - x
Third quadrant is 180 + x
Fourth quadrant is 360 - x

Look at a unit circle and this will make sense. x is an acute angle.

sin30 = sin30 and sin(180-30) = sin150

 

[braintic]

.... sin is positive in A and S ....

Huh?

 

[VBN2470]

Huh?

ATSC (All Stations To Central):

In Quadrant I: A for All - all trigonometric functions are positive in this quadrant.
In Quadrant II: S for Sine - sine and cosecant functions are positive in this quadrant.
In Quadrant III: T for Tangent - tangent and cotangent functions are positive in this quadrant.
In Quadrant IV: C for Cosine - cosine and secant functions are positive in this quadrant.

http://en.wikipedia.org/wiki/All_Students_Take_Calculus

 

[braintic]

ATSC (All Stations To Central):

In Quadrant I: A for All - all trigonometric functions are positive in this quadrant.
In Quadrant II: S for Sine - sine and cosecant functions are positive in this quadrant.
In Quadrant III: T for Tangent - tangent and cotangent functions are positive in this quadrant.
In Quadrant IV: C for Cosine - cosine and secant functions are positive in this quadrant.

http://en.wikipedia.org/wiki/All_Students_Take_Calculus

Ummmm ..... you know I'm a maths teacher, right?
A, S, T, C are not the names of the quadrants - "sin is positive in A and S" makes no sense.
It's like taking ROYGBIV and saying "Green is the g-th colour of the rainbow".

 

[VBN2470]

Ummmm ..... you know I'm a maths teacher, right?
A, S, T, C are not the names of the quadrants - "sin is positive in A and S" makes no sense.
It's like taking ROYGBIV and saying "Green is the g-th colour of the rainbow".

Yeah, I think the OP knows that but he mistakenly wrote it down, since he was probably trying to recall which quadrants are positive for which functions and just rushed his post. Obviously, in the real HSC (and even in school exams) what the OP stated (i.e "sin is positive in A and S") won't be accepted, since it's not mathematically sound and markers wouldn't even understand what it would mean too (he should have written "sin is positive in quadrants 1 and 2"). LOL, I thought you didn't know what ATSC was (hence why I replied with my post), as opposed to you actually questioning the validity of the statement the OP posted

 

[Crisium]

Yeah, I think the OP knows that but he mistakenly wrote it down, since he was probably trying to recall which quadrants are positive for which functions and just rushed his post. Obviously, in the real HSC (and even in school exams) what the OP stated (i.e "sin is positive in A and S") won't be accepted, since it's not mathematically sound and markers wouldn't even understand what it would mean too (he should have written "sin is positive in quadrants 1 and 2"). LOL, I thought you didn't know what ATSC was (hence why I replied with my post), as opposed to you actually questioning the validity of the statement the OP posted

Yeah the bolded part is the best way to go

Although I have seen in many papers that you can get away with using ASTC as long as you draw up the axis with four quadrants and label them with their respective letter and whether it is 180 - x, 360 - x, etc.

 

[applebeeby]

Don't take the inverse to start with. Divide both sides by sqrt3. So tanx=-1/sqrt3
Then find the reference angle (use the triangles).
Look at which quadrants tan is negative in, as it is -1/sqrt3

 

[milkytea99]

Answer is D.

 

[milkytea99]

Since it's -30. It means tan is negative, so in ASTC, you choose the 2nd and 4th quadrant. 2nd quadrant is 180-30 which is 150, and 4th is 360-30, which is 330. Then convert 150 and 330 into radians and answer is D

 

[BlueGas]

I need help with another question, is the way I worked out this question right?

 

[InteGrand]

I need help with another question, is the way I worked out this question right?

There should be two solutions for . You were meant to do 180º + (-63)º, and 360º + (-63)º for that.

So answer is that there are three solutions.

Alternatively, just sketch graphs of the two functions in the given domain. We can see then that the horizontal line intersects that of in two places in the given domain, and the line of touches the graph of exactly once in the given domain. Hence answer is 3.