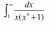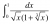Make a Difference – Donate to Bored of Studies!
Students helping students, join us in improving Bored of Studies by donating and supporting future students!
HSC 2012-14 MX2 Integration Marathon (archive) (3 Viewers)
- Thread starter bleakarcher
- Start date
- Status
- Not open for further replies.
Re: MX2 Integration Marathon
Then the integral is reduced to 6u^2/(1+u^2), factor out constants, +1-1 and you get a 6 as a constant and a tan inverse integration (of 1=pi/4)...
=6*(1-pi/4)
=6-2pi/3
Nice shifty U-sub haha
By inspection if we expand the bottom the power of x will be 5/6. Hence let u=x^1/6
Then the integral is reduced to 6u^2/(1+u^2), factor out constants, +1-1 and you get a 6 as a constant and a tan inverse integration (of 1=pi/4)...
=6*(1-pi/4)
=6-2pi/3
Nice shifty U-sub haha
Re: MX2 Integration Marathon
1/infinity=0
Hence = 1/n * [ln(1)-ln(1/2)]
=1/n * ln(1/2)
This time let u=x^n+1, do some partial fractions, inside the log you can split into 1-1/u which when put under boundaries of 2 to infinity...
1/infinity=0
Hence = 1/n * [ln(1)-ln(1/2)]
=1/n * ln(1/2)
faisalabdul16
Wot
- Joined
- Feb 16, 2014
- Messages
- 2,256
- Gender
- Male
- HSC
- 2014
Re: MX2 Integration Marathon
I did two substitutions lol. Nevertheless got the same answer.
Nice !By inspection if we expand the bottom the power of x will be 5/6. Hence let u=x^1/6
Then the integral is reduced to 6u^2/(1+u^2), factor out constants, +1-1 and you get a 6 as a constant and a tan inverse integration (of 1=pi/4)...
=6*(1-pi/4)
=6-2pi/3
Nice shifty U-sub haha
I did two substitutions lol. Nevertheless got the same answer.
integral95
Well-Known Member
- Joined
- Dec 16, 2012
- Messages
- 776
- Gender
- Male
- HSC
- 2013
Re: MX2 Integration Marathon

} = \frac{sin^2x+cos^2x}{{cosx(cosx-sinx)}} = \frac{cosx +sinx}{cosx - sin x} - \frac{sinx}{cosx} \\ \\ \therefore \int\frac{2}{2cos^2x-sin2x} = \int \frac{cosx +sinx}{cosx - sin x} - \frac{sinx}{cosx} = -ln(cosx - sinx) + ln(cosx) \\ \\ \\ = ln(\frac{cosx}{cosx - sinx}) )
Well the hard part is the integral really so i'll just do thatHehe made an easy q, What is this to 2 dp:
)
integral95
Well-Known Member
- Joined
- Dec 16, 2012
- Messages
- 776
- Gender
- Male
- HSC
- 2013
Re: MX2 Integration Marathon
^2)+4)^2} \\ \\ \\ $Let x+1 = tan\theta$ \\ \\ 2\int_{0}^\frac{\pi}{4}\frac{(2tan\theta-1)sec^2\theta}{16sec^4\theta} \\ \\ = \int_{0}^\frac{\pi}{4}\frac {2tan\theta-1}{8sec^2\theta} = \frac{1}{4}\int_{0}^\frac{\pi}{4}sin\theta cos\theta d\theta \ - \frac{1}{8}\int_{0}^{\frac{\pi}{4}} cos^2\theta d\theta \\ \\ = \frac{1}{8}\int_{0}^{\frac{\pi}{4}}sin2\theta -cos^2\theta \ d\theta \\ \\ = \frac{-1}{16}[cos2\theta + \theta + \frac{1}{2}sin2\theta] = \frac{1}{16} - \frac{\pi}{64} )
I wanna do itHere's an actual challenging Q: (Well not for you guys ofcourse)
^2}dx)
nightweaver066
Well-Known Member
- Joined
- Jul 7, 2010
- Messages
- 1,585
- Gender
- Male
- HSC
- 2012
Re: MX2 Integration Marathon
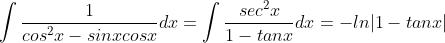
An easier way..Hehe made an easy q, What is this to 2 dp:
)
dan964
what
Re: MX2 Integration Marathon
Integrate e^(xe^(x^2))
Integrate e^(xe^(x^2))
Last edited:
Re: MX2 Integration Marathon
So that's e to the power of e to the power of e^x squared, hmm does that work?Integrate e^(xe^(x^2))
Carrotsticks
Retired
- Joined
- Jun 29, 2009
- Messages
- 9,467
- Gender
- Undisclosed
- HSC
- N/A
Re: MX2 Integration Marathon
Yep, look up "Power Towers" in google.So that's e to the power of e to the power of e^x squared, hmm does that work?
dan964
what
Re: MX2 Integration Marathon
No it is e to the power of x times e to the power of x^2So that's e to the power of e to the power of e^x squared, hmm does that work?
- Status
- Not open for further replies.