Re: HSC 2013 4U Marathon
Fun little question.
a) A whole grade consisting of several (>1) classes participates in a mathematics competition. In each class the average female score is higher than the average male score. Is it possible for the average male score over the entire grade to be higher than the average female score over the entire grade?
b) What if all classes are the same size?
c) What if each class has an equal gender ratio?
Justify all answers with either a proof or a counterexample.
(Nothing too difficult, perhaps more apt for the 2U or 3U forum but I think its cool.)
I am going to answer the parts of this question in seperate posts as I solve them:
a) Yes, it is possible for the average male score to be higher than the average female score over the entire grade.
This is quite easy to see actually. The average male/female score of each class has a certain "weighting". The more students of one gender there is, the stronger the weighting of the class average. For example, a class consisting of 2 boys and 2 girls will have a far less affect on the entire cohort compared to a class of 20 boys and 20 girls, and hence the larger class has a higher "weighting".
Therefore it should be easy to see why this situation is possible. All we have to do is let the male "weighting" of one class absolutely dominate the female "weighting", and let the rest of the remaining classes have a very small "weighting". As a general counterexample:
Let the first class have

amount of boys, and

girls. Give the restriction
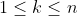
Suggest now that there are
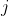
other classes, all containing
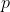
amount of boys and girls.
All we need to do is make the variables
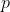
as small as we like in realistic terms, and make

as big as we like, and the "weighting" of

will reach a certain point where it dominates the combined weighting of the other variables, and hence the average male score over the entire grade will be higher than the average female score.
